Точные измерения отражения и пропускания высокорефрактивных материалов
|
Точное определение абсолютных значений пропускания и отражения значений в ИК-диапазоне является предметом растущего интереса, например, при разработке оптических фильтров, зеркал или оконного стекла, а также в ряде направлений исследований. Bruker Optics предлагает специализированные приборы для точных измерений как отражения, так и пропускания.
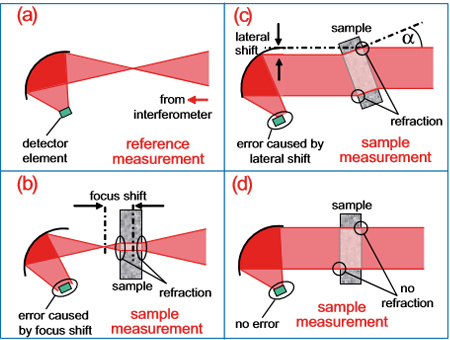
Рис. 1(а) и (b): Конструкция стандартных приборов для измерения пропускания и присущие им погрешности. 1(с): косой угол падения приводит к погрешности из-за бокового сдвига пучка. 1(d): Обе погрешности можно исключить с помощью параллельного пучка и прямого угла падения. Именно эта концепция реализована в приборе пропускания параллельного пучка A480, показанном на рис. 2. Особенно в высокорефрактивных (а следовательно, отражающих) образцах (например, полупроводниках), падение под прямым углом может вызывать дополнительные сложности. ИК-свет, отраженный образцом, может привести к артефактам, вызванным так называемой двойной модуляцией. В спектрометрах Bruker Optics, таких как VERTEX 70 или TENSOR 27/37, основанных на интерферометре RockSolid с так называемыми кубическими уголковыми зеркалами, эта задача решается путем использования уменьшенной вдвое диафрагмы (см. рис. 3). Однако эффекта двойной модуляции можно избежать и в спектрометрах, основанных на интерферометре с линейным движением зеркала и плоскими зеркалами (например, серия VERTEX80). В этом случае половина промежуточного фокуса блокируется диафрагмой с острым краем, что обеспечивает точное измерение пропускания (см. прибор A480/8 для серии VERTEX80).
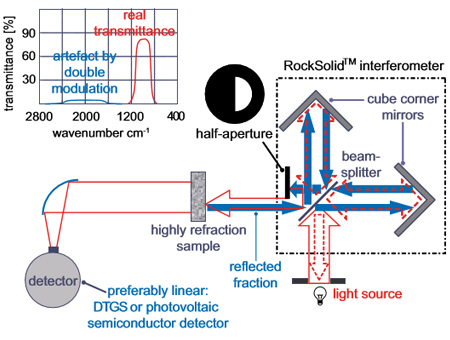
Рис. 3: Схематическое изображение блокирования дважды модулированного света (синие стрелки) уменьшенной вдвое диафрагмой между интерферометром RockSolid и отсеком для образца. Без мер предосторожности двойная модуляция может вызвать артефакты, например показанные в верхнем левом углу (при использовании полосового фильтра). В качестве примера, на рис. 4 показан коэффициент пропускания полосового фильтра, измеренный с использованием прибора A480. Так как за пределами спектрального окна между 2600-3000 см-1 коэффициент пропускания должен быть равен нулю, этот пример хорошо подходит для проверки точности в случае нулевого коэффициента пропускания. Нулевой коэффициент пропускания полосового фильтра может быть точно воспроизведен с отклонением ≤ 0,01% (рис. 4). Чтобы проверить точность прибора A480 при абсолютных значениях коэффициента пропускания, отличных от нуля, нужен образец, коэффициент пропускания которого известен как можно более точно. Для этого мы использовали полупроводник германий: показатель преломления, установленный экспериментальным путем, составляет nGe ≈ 4,003 при 1000 см-1 [1, 2]. Если использовать уравнения Френеля с несколькими внутренними отражениями, это соответствует теоретическому коэффициенту пропускания примерно 47,03% при 1000 см-1. Экспериментальные результаты в отношении германия (показаны на рис. 5) хорошо согласуются с этими допущениями. Выше зоны поглощения германия (≈ 5800 см-1) коэффициент пропускания должен быть равен нулю. Это подтверждается экспериментальным путем, как показано на рис. 6. Прибор для определения абсолютного коэффициента отражения A519 В стандартных приборах значение отражения образца, как правило, определяется как отношение одноканального спектра, отраженного образцом, и одноканального спектра, отраженного эталонным зеркалом. Этот метод подходит для многих решения многих задач, т.к. он выявляет все важные спектральные особенности, но при определении абсолютного коэффициента отражения неизбежна определенная погрешность. Получаемые абсолютные величины верны, только если коэффициент отражения эталонного зеркала точно равен 100%. В действительности, фактический коэффициент отражения обычного (покрытого золотом) зеркала составляет около 99% и демонстрирует небольшую (плоскую) спектральную зависимость. Возможны дополнительные отклонения из-за царапин или посторонних частиц на поверхности (напр., пыль). В целом, существует два подхода к устранению этого источника погрешности: Во-первых, с помощью калиброванного эталонного зеркала, погрешность можно устранить, опираясь на фактическое отражение зеркала. Эту процедуру можно автоматизировать с помощью соответствующего макроса OPUS. Тем не менее, многие пользователи избегают этого метода, поскольку калиброванные зеркала являются дорогостоящими и требуют обращения с особой осторожностью во избежание изменений отражательной способности. Если важны точные абсолютные значения, зеркало необходимо регулярно калибровать, чтобы учесть изменения отражательной способности с течением времени.
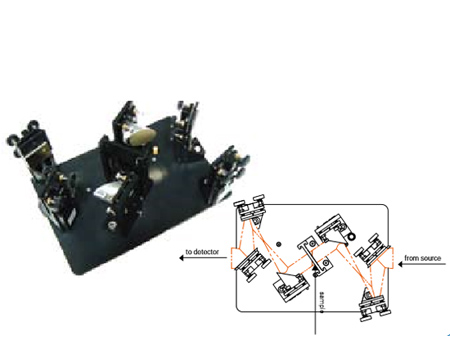
Рис. 7: Схематическая траектория луча и фотография прибора A519 для измерения абсолютного коэффициента отражения. Чтобы устранить указанную выше погрешность, Bruker Optics разработала прибор А519 для измерения абсолютного коэффициента отражения (см. рис. 7) без использования калиброванного зеркала. Это возможно потому, что эталонное зеркало также является частью траектории луча. Поэтому, если использовать отношение эталонного и фактического значений, отражательная способность зеркала устраняется и не влияет на результат. Прибор включает эталонное зеркало и может использоваться для измерения эталона и образца с помощью измерительной головки высокой точности, которая может поворачиваться на 180°. Как показано на рис. 8, для измерения образца инфракрасный луч отражается дважды в двух разных точках образца (расстояние 22 мм; угол падения 11°). Для однородных образцов результат равен квадрату R2 отражательной способности образца. Абсолютный коэффициент отражения определяется путем вычисления квадратного корня результата измерения с помощью программного обеспечения. Для неоднородных образцов результатом процедуры является средняя абсолютная отражательная способность R1/2. Для проверки точности A519 мы использовали другой полупроводник - кремний. При показателе преломления nSi = 3.417 [2] теоретический коэффициент отражения кремния должен составить ≈ 46,09% при 2000 см-1. На рис. 9 показан абсолютный коэффициент отражения образца кремния, определенный с помощью прибора A519. Наблюдаемое небольшое отклонение ≈ 0,3% не обязательно является погрешностью измерения и может быть результатом незначительной погрешности в использованном коэффициенте преломления. Если повысить nSi на 0,02 до nSi = 3,44, теоретический коэффициент отражения составит 46,4%. Удобный метод исследования, который не зависит от опубликованных коэффициентов преломления и основан на применении приборов A480 и A519, заключается в следующем: Из физики полупроводников известно, что выше 1800 см-1 кремний не поглощает свет, так как инфракрасные активные колебания решетки имеют более низкую энергию. Поскольку исследуемый образец имел высокое качество поверхности, потерями на рассеяние можно пренебречь, и следовательно, сумма коэффициентов пропускания и отражения должна быть 100%. На рис. 10 показан коэффициент пропускания Si, измеренный A480, коэффициент отражения Si, измеренный A519, и их сумма. Наконец, на рис. 11 показано, что в области нулевого поглощения выше 1800 см-1 сумма коэффициентов отражения и пропускания очень близка к теоретическому значению 100%. В целом, точность обоих рассмотренных приборов зависит от исследуемого образца. Как можно увидеть из примеров, используя оптимизированные компоненты, можно добиться точности выше 0,25%. Список использованной литературы: [1] “Handbook of Optics”, 2nd Edition, Vol. II (McGraw-Hill,1995) [2] Online database of “Korth Kristalle GmbH”; www.korth.de |
Прибор с параллельным лучом для измерения коэффициента пропускания А480 В традиционных приборах для измерения пропускания образец обычно помещается в фокусе ИК-луча, как показано на рис. 1 (а) и (b). При исследовании толстых и высокорефрактивных образцов, преломление вызывает сдвиг ИК-фокуса в сторону приемника, что вызывает погрешность в определении коэффициента пропускания (см. рис. 1 (b)). При наклонном падении луча преломление приводит к возникновению дополнительной погрешности, вызванной боковым смещением луча (рис. 1 (с)). Эти погрешности можно устранить, исследуя образец в параллельном ИК-луче с прямым углом падения, как показано на рис. 1 (d).
Рис. 2: Схематическое изображение траектории луча и фотография прибора с параллельным лучом для измерения коэффициента пропускания А480.
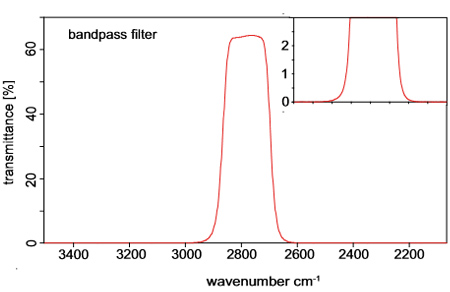
Рис. 4: Пропускание полосового фильтра, измеренное с помощью прибора A480, интерферометра VERTEX 70 и приемника из дейтерированного триглицидил сульфата (DTGS). Как видно на вставке, за пределами диапазона пропускания достигается номинальное значение, равное нулю.
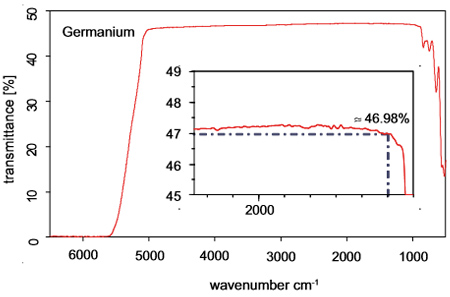
Рис. 5: Пропускание двустороннего полированного образца германия, измеренное с помощью прибора A480, интерферометра VERTEX 70 и приемника из дейтерированного триглицидил сульфата (DTGS). Поскольку образец довольно толстый (6 мм), при использованном спектральном разрешении 4 см-1 отсутствуют какие-либо интерференционные полосы. На вставке видно, что в средней ИК области спектра (1000 см-1) практически воспроизводится теоретический коэффициент пропускания.
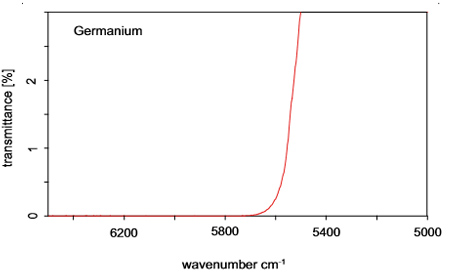
Рис. 6: Пропускание германия, измеренное с помощью прибора A480 и интерферометра VERTEX 70. Благодаря его более высокой чувствительности в ближней ИК области в данном случае был использован приемник InGaAs. В соответствии с теоретическими расчетами, пропускание выше зоны поглощения оказалось равным нулю с отклонением << 0,1%.
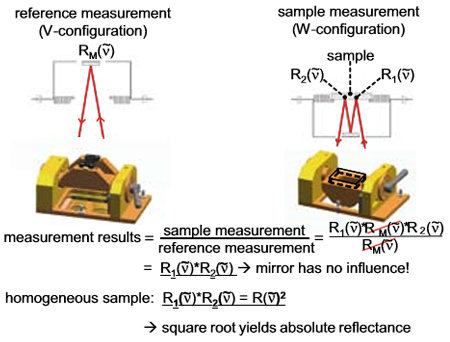
Рис. 8: Принцип действия прибора для измерения абсолютного коэффициента отражения A519. Поскольку эталонное зеркало (для измерения абсолютного коэффициента отражения) является частью траектории луча при исследовании как эталона, так и образца, оно не оказывает никакого влияния на R2 (и соответственно, R1*R2 в неоднородных образцах).
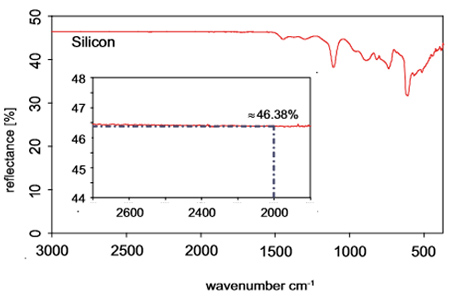
Рис. 9: Абсолютный коэффициент отражения толстого двухстороннего полированного образца кремния, измеренный с помощью прибора A519, интерферометра VERTEX 70 и приемника из дейтерированного триглицидил сульфата (DTGS).
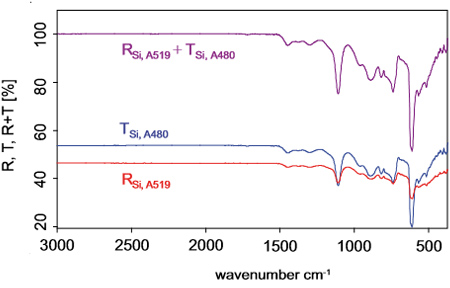
Рис. 10: Коэффициент отражения Si (красный, измерен A519), коэффициент отражения Si (синий, измерен A480) и их сумма (фиолетовый). Все спектры определены с помощью VERTEX 70 и приемника DTGS.
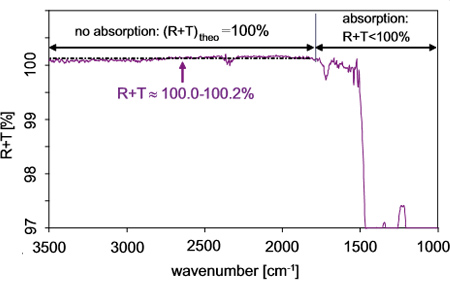
Рис. 11: Сумма коэффициента пропускания и коэффициента отражения кремния, измеренная с помощью обоих описанных приборов, VERTEX 70 и приемника DTGS. В зоне нулевого поглощения выше 1800 см-1 в довольно хорошем приближении достигнуто теоретическое значение 100%. |